Understanding Risk - How Investors should think about Risk
Discover more from The All-in-One Investing Newsletter
Understanding Risk - How Investors should think about Risk
Why should Investors care about Risk?
An investor’s goal is to make money. If you’re a smart investor, you also know that the best way to do that is to compound your money over a long period of time.
The main rule to do so is to never lose money.
Buffett once said:
“There are two rules to investing. Rule number one: Never lose money. Rule number two: Never forget rule number one.”
Never losing money is so important because there’s nothing more harmful to compounding than interrupting that process by experiencing a severe loss.
And loss is a great keyword to really get into risk.
What is Risk?
In academia, risk is called volatility and measures the range of fluctuations over a period of time.
But for an investor, this definition of risk seems insufficient. If I know that I’ll turn $1000 into $10,000 in the next 5 years, then I don’t really care about volatility (assuming that liquidity is not an issue).
But why is volatility used if it’s insufficient in explaining risk?
The answer is pretty straightforward, it’s quantifiable. And academia needs to quantify risk to come up with their theories.
“Volatility can be an indicator of the presence of risk - a symptom - but it is not risk itself.” - Howard Marks
But what is risk?
Risk is the probability of a permanent loss of capital.
Permanent is important here. If you buy an index representing the market, downturns will (with as much certainty as you can have) be temporary. Until today, the MSCI World has always recovered from its drawdowns, no matter how severe.
Individual companies don’t act that way. They come and go. Some strive, some die. And if you bet on the wrong company, your investment is gone. Permanently.
This is the risk an investor faces every day.
Understanding the Uncertainty that comes with Risk
“There is a range of outcomes, and we don’t know where the actual outcome is going to fall within the range. Often, we don’t know what the range is.” - Peter L. Bernstein
We can think about the future as a probability distribution, and we never know which outcome will happen.
We wouldn’t even know if we knew the exact probabilities and all possible outcomes.
The most unlikely things happen all the time, and the most certain things fail to happen all the time.
‘We live in the sample, not the universe.” - Chris Geczy
The markets are a great example of that. A reason for that is the behavior of the market participants.
The risk of an activity often lies in the behavior of participants, not the activity itself.
When investors think there’s no risk involved, usually at the market top, the risk is the greatest. The same goes for downtrends. The higher the perceived risk, the lower the actual risk.
The Relationship between Risk and Return
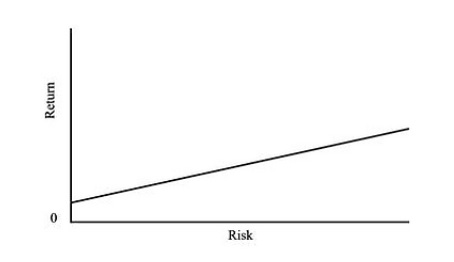
At business school, you will see the graphic below a lot. It indicates a positive relationship between risk and return.
The more risk you take, the higher your return will be. This doesn’t sound right, does it?
That’s because the “risk” mentioned in this graph is volatility, as we discussed in the beginning.
But we are smarter now and know that risk is the possibility of permanent loss of capital and the uncertainty that comes with all the possible outcomes.
Yet, the graph below isn’t completely wrong. In general, investments with higher uncertainty produce higher returns. And higher uncertainty also means higher risk.
But how can we upgrade this graph so that uncertainty and the risk of losing money become more clear?
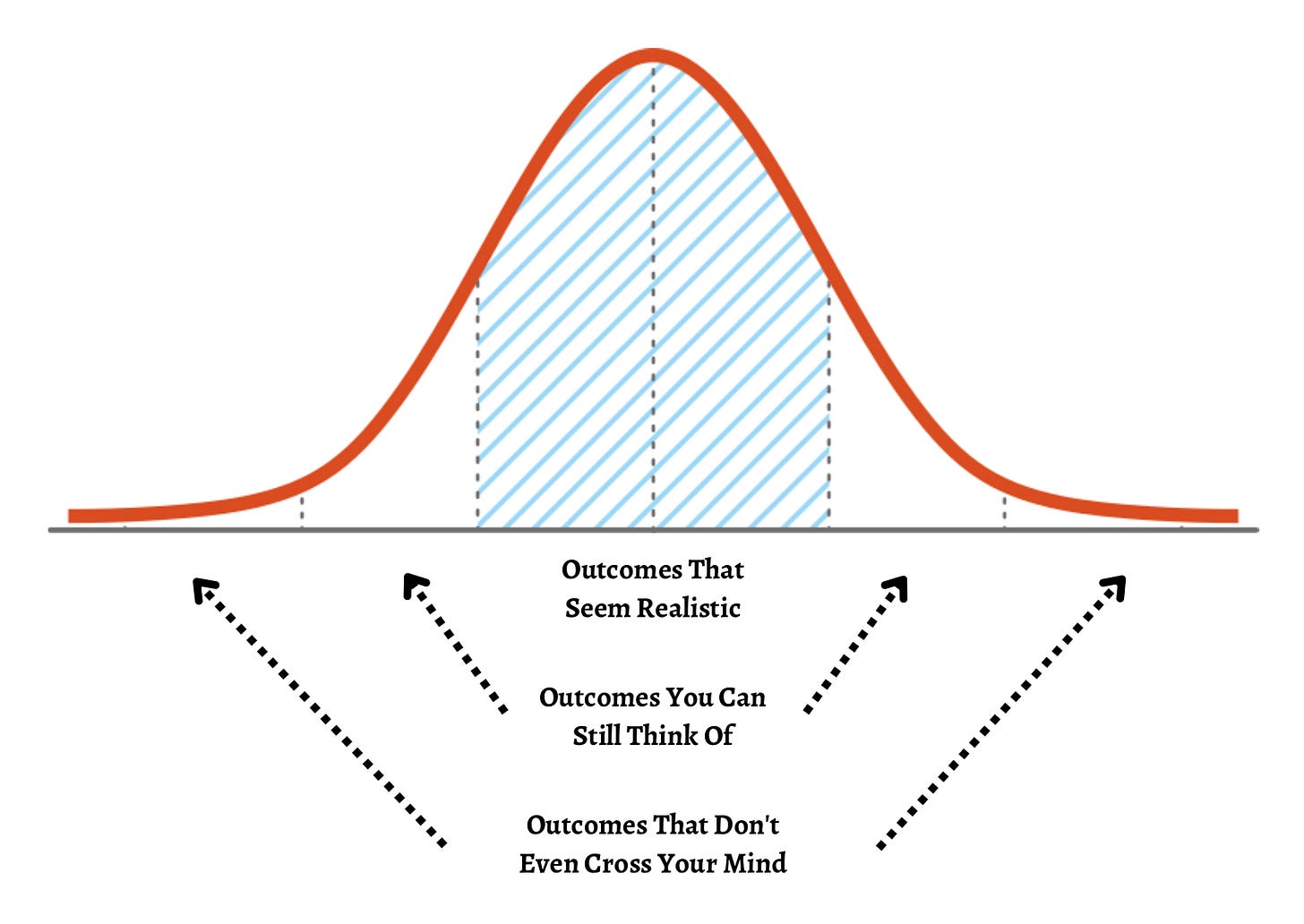
Howard Marks comes up with the graph below. You still see the same line as within the traditional theory since the idea of higher returns demanding higher risk is, more or less, right.
But now you can see bell-shaped curves that represent the uncertainty of outcomes. The more risk you take, the less certain the outcomes get and the worse the outcomes can become.
Knowing about what risk is and the relationship between risk and return, let’s discuss how investors should go about handling risk.
How should Investors handle Risk?
Think of investment performance as pulling a ticket out of a bowl filled with hundreds of tickets. All of these tickets represent different outcomes. But the only one that matters is the one you pulled out of that bowl.
The task of the investor is to know about as many tickets (outcomes) as possible, how likely they are (not precisely but vaguely), and what each outcome would mean for their investment.
Obviously, you can’t know any of that. But superior investors stand out for having a better-than-average sense of the tickets in that bowl and their possible consequences.
Joel Greenblatt talks about context when analyzing companies. The same context plays a role in managing risks.
The best investors are great at putting things into perspective.
But what can we do to improve our senses?
There are a variety of ways to improve our senses and to get better at putting things into perspective. Here are the 3 most important ones:
Psychological Biases
One reason why we misjudge risk are biases that distort our perception of risk and do not allow us to make rational decisions. If you want to learn more about such biases, there’s a link to an article I wrote on biases below.
Learning about History
History doesn’t repeat itself, but it rhymes. When assessing risk, it makes sense to look at history and find instances in which something similar happened. How did that scenario play out, and what can you learn from it?
Understanding Risk
Obviously, understanding risk is also crucial in assessing it. That’s why I wrote this article in the first place.
Conclusion
Risk cannot be measured, which makes it extremely hard to assess risk, both in the future and even in the past.
As an investor, you need to be aware that you’ll never know about all possible outcomes and that it’s impossible to be certain about anything.
Your challenge is to be prepared for outcomes you were unaware of before and survive them when they occur.
One key element of investing is looking for asymmetrical bets. Bets that have unlimited upside but limited downside.
Mohnish Pabrai used to say: “Heads, I Win; Tails, I Don't Lose Much.”
But asymmetric bets will be discussed in a later article.
Thanks a lot for taking the time to read this. I hope you learned something new.
If you did, consider following my Substack and my Twitter to keep up to date with my latest posts.
Understanding Risk - How Investors should think about Risk
Fantastic, illuminating and enlightening piece.
In 'Elements of Successful Trading', Robert Rotella described risk as being a function of the amount of loss and the probability of experiencing that loss. So that means an asymmetric bet is not necessarily one involving unlimited upside and limited downside, but one where the probability-adjusted reward-to-risk is in one's favour. This is a more realistic approach.
Another consideration - note in Howard Mark's version of the reward-to-risk graph, the line corresponding to the mean of each distribution of outcomes is placed on the reward-to-risk line. This reflects the effect of the central tendency measure, which is influenced by the frequency of outcomes at the mean.
In a normal distribution, which is the one being represented in the graph, the greatest frequency of outcomes is at the mean. But in finance, most market distributions are not normal; they are leptokurtic, meaning they have excess kurtosis, which may or may not be to a degree that's significantly different than normal.
And they tend to be skewed. Both of these moments imply greater frequency than normal of outcomes in the 'tails' and on one side of the distribution, respectively. And skew may or may not be to a degree that is significantly different than normal. But if a distribution is significantly different than normal, the 'Z' scores corresponding to probable outcomes loses its effectiveness.
Thus, while standard deviation is a decent measure of volatility it's a lousy measure of potential risk, which is better defined by the moments of skew and kurtosis (especially). Hence the increasing adoption of measuring for the risk of 'fat tails' and awareness of skewness.
A good example of risk mis-underestimation is in the shares of AI darling, Nvidia.
Going into its late May'23 earnings release, various popular measures of risk ranged from about +/-6-7% using ATM straddle options implied move to -9-11% using parametric and historical Value-at-Risk or VaR (even at the 99%, one-tailed confidence interval).
In the event, shares popped 25% on the day, equivalent to if I recall correctly without checking, a nearly 7 standard deviation move encompassing daily returns data since the company's public listing inception in 1999.
What made this particularly tragic was, in my opinion, that the stock had just recently before its earnings completed a textbook upwards measured move out of a bullish (inverted) head and shoulders pattern on its weekly chart, likely prompting many bears to position short, whether in shares or options.
If you were short, and were only expecting what these measures suggested, the pain was palpable.
You might say, 'Right then; there's no value in attempting to measure risk at all'. But that would be a mistake. Rather, you have to make sure you understand what the measure of risk you're using is actually doing. And try to get a picture of as much data as possible.
Looking at a distribution of the entirety of Nvidia's actual daily returns going into its earnings revealed positive skew, albeit not significantly different than normal; but excess kurtosis that was significantly different than normal. So - there was fat tail risk, and it was to the upside.
Visually inspecting the distribution and a graph of past actual daily returns prior to the earnings revealed that Nvidia indeed had some extreme upside days in its past, at least one if not two exceeding its 25 May'23, +25% percentage change. They just hadn't occurred in close time proximity, which reveals yet another weakness with typical risk estimation - recency bias.
We humans tend to conceptualise around only the previous five years (at best). And that recency bias is reflected in the typical lookbacks used in summary statistics. For example, within the Portfolio Risk function on even the vaunted Bloomberg Professional terminal, VaR tab, estimates for historical (non-parametric) VaR using confidence intervals of 95%, 97.5% and 99% are calculated for only 1, 2 or 3-year lookbacks.
The old saying goes, 'Anything's possible, but not everything is probable'. And it is on this maxim that most risk estimation leans. But knowing what's possible is perhaps more important than knowing what's probable, especially if the returns profile of an asset reduces the relevance of the probability values associated with that asset's distribution. This is especially so as even knowing what's possible from past data is at best a sample, as you point out in the article.
The reality is that the most nimble, consistently profitable operators in the markets are using proprietary models that are far more sophisticated than the ones in the public domain, with most of the public not even using those, and this is what differentiates their performance versus the public's results.
While sobering, that's not reason alone to abstain completely from trading or investing, but rather to realise that the models you're leaning on have flaws. One way of minimising the potential shortcomings is to not use summary statistics in isolation, but augment them with visual inspection of the data and adjust exposures to levels commensurate with what's really possible.
This reckoning will de facto result in being more selective in choosing opportunities and cautious in the size and directional bias of positioning, hopefully improving overall outcomes over time.
Looking at your 'About', I must say it is rare to see a college student with your level of enthusiasm for the markets and all things investing/trading, as embodied in this blog. Something tells me, you'll be going far. ;-)